- Calculs théoriques
- Application concrète
- Conclusions
- Annexes
Notre idée en bref
L'idée est de prendre un patator, objet connu comme étant une source d'amusement, et d'examiner son fonctionnement d'un oeil scientifique. Pour ce faire, il faut étudier tous les aspects de cette arme dont nous pourrions parler, puis expliquer tous les phénomènes qui rentrent en jeu dans le processus qui permettra de projeter la pomme de terre dans les airs.
Nous avons donc commencé par réaliser des calculs théoriques. Ces derniers étant complexes, nous avons eu besoin de l'aide de nos professeurs pour en venir à bout. Notamment dans le cadre des dérivés, chapitre que nous n'avions pas étudié au moment de faire ces calculs, et pour les calculs de physique-chimie, qui ne sont pas au programme de première scientifique. Nous avons donc, le calcul de l'énergie libérée par une combustion, le calcul de la vitesse théorique de sortie de la pomme de terre, et le calcul de l'équation cartésienne de la parabole décrite par le projectile.
Energie libérée par les gaz
La première chose à calculer est l'énergie libérée lors de la combustion des gaz puisque, comme nous l'avons expliqué dans notre introduction, le patator se sert de la pression générée par la chaleur inhérente à la combustion du gaz qui se trouve dans la chambre de combustion pour expulser le projectile. Pour ce faire, il faut faire la différence entre les énergies de liaison qui composent les réactifs et celles que contiennent les produits. Nous avons donc dû trouver un tableau des énergies de liaison qui nous permettrait par la suite d'effectuer ces calculs. Ainsi, nous avons réfléchi aux trois gaz les plus courants, à savoir le méthane, le propane et le butane.
Le méthane
L'élément chimique méthane a pour formule brute CH4.
On a donc quatre liaisons Hydrogène-Carbone de 410 kJ/mol.
La réaction entre le méthane et le dioxygène (une double liaison Oxygène-Oxygène de 494 kJ/mol) produit du dioxyde de carbone CO2 et de l'eau H2O (deux doubles liaisons Carbone-Oxygène de 795 kJ/mol et deux liaisons Hydrogène-Oxygène de 460 kJ/mol)
En équilibrant l'équation chimique, on a :
CH4 + 2 O2 → CO2 + 2 H2O
Le calcul revient à faire:
Q= [4(C-H) + 2(O=O)] – [2(C=O) + 2x2(H-O)]
Q= (4x410 + 2x494) – (2x795 + 4x460)
Q= -802 kJ/mol
L'énergie libérée par une combustion de méthane et de dioxygène est donc de 802 kJ par mole de gaz.
Le propane
L'élément chimique propane a pour formule brute C3H8 .
On a donc huit liaisons Hydrogène-Carbone de 410 kJ/mol et deux liaisons Carbone-Carbone de 348 kJ/mol.
La réaction entre le propane et le dioxygène (une double liaison Oxygène-Oxygène de 494 kJ/mol) produit du dioxyde de carbone CO2 et de l'eau H2O (deux doubles liaisons Carbone-Oxygène de 795 kJ/mol et deux liaisons Hydrogène-Oxygène de 460 kJ/mol)
En équilibrant l'équation chimique, on a:
C3H8+ 5 O2 → 3 CO2 + 4 H2O
Le calcul revient à faire:
Q= [8x(C-H) + 2x(C-C) + 5x(O=O)] – [3x2(C=O) + 4x2(H-O)]
Q= (8x410 + 2x348 + 5x494) – (6x795 + 8x460)
Q= -2 004 kJ/mol
L'énergie libérée par une combustion de propane et de dioxygène est donc de 2 004 kJ par mole de gaz.
Le butane
L'élément chimique butane a pour formule brute C4H10.
On a donc dix liaisons Hydrogène-Carbone de 410 kJ/mol ; trois liaisons Carbone-Carbone de 348 kJ/mol.
La réaction entre le butane et le dioxygène (une double liaison Oxygène-Oxygène de 494 kJ/mol) produit du dioxyde de carbone CO2 et de l'eau H2O (deux doubles liaisons Carbone-Oxygène de 795 kJ/mol et deux liaisons Hydrogène-Oxygène de 460 kJ/mol).
En équilibrant l'équation chimique, on a :
2 C4H10 + 13 O2 → 8 CO2 + 10 H2O
Le calcul revient à faire:
Q= [2x10(C-H) + 2x3(C-C) + 13(O=O)] – [8x2(C=O) + 10x2(H-O)]
Q= (20x410 + 6x 348 + 13x494) – (16x795 + 20x460)
Q= -5 210 kJ/mol
L'énergie libérée par une combustion de butane et de dioxygène est donc de 5 210 kJ par mole de gaz.
Choix du gaz
On remarque que le gaz qui dégage le plus d'énergie est le butane ; c'est pourquoi nous choisirons ce gaz pour une portée optimale de nos tirs.
Volume du gaz à injecter
Avant toute chose, il est nécessaire de déterminer le volume de butane à injecter dans la chambre de combustion pour que les réactifs soient stoechiométriquement proportionnés et que la combustion dégage ainsi une énergie aussi élevée que possible. Pour ce faire, il faut dans un premier temps connaître le volume de la chambre, puis la proportion de butane qui réagit avec le dioxygène lors de la combustion, et enfin, les quantités de matière qui seront en contact avant la combustion ainsi que celles qui seront produites par celle-ci.
Volume de la chambre de combustion
La chambre de combustion est un cylindre de 70 cm de long sur 10 cm de diamètre. Donc son volume est :
V = ∏r2 h
V = ∏(0.05)2 x 0.70
V = 5.5L
On sait donc que le cylindre qu'est la chambre de combustion a un volume de 5.5 litres.
Volume de butane à injecter
On sait qu'il faut 13 moles de dioxygène pour faire brûler 2 moles de butane. De même que l'on connait la proportion de dioxygène dans l'air (21%). Or tous les gaz ont le même volume molaire qui est de 24 L/mol. Donc il faudra deux treizièmes du volume de dioxygène de butane à l'intérieur de la chambre de combustion pour que les réactifs de la combustion soient stoechiométriequement proportionnés. En sachant que le gaz sera injecté sous pression dans le patator, on peut donc en déduire qu'il y aura besoin de deux treizièmes de 21% de 5.5L de butane, soit 0.18L. Afin de pouvoir injecter avec précision cette quantité de gaz, il nous faudra avoir recours à un manomètre pour nous indiquer la variation de presssion qui a lieu lors de l'introduction de gaz. Ainsi, une augmentation de 0.18L sur un volume initial de 5.5L génère une pression de 1.03 bar environ. Il faudra donc que le manomètre affiche cette pression au minimum pour que la combustion libère l'énergie que nous allons calculer ci-après.
Quantité de matière correspondante
Le volume molaire des gaz étant de 24 L/mol, la quantité butane dans la chambre de combustion vaut 0.18/24 et celle de dioxygène 1.155/24 , soit respectivement environ 7.5 x 10-3 moles de C4H10 et 4.8 x 10-2 moles d'O2.
Vitesse théorique initiale de la pomme de terre
Maintenant que la quantité de butane présent pour la combustion est connue, on peut en déduire (ou plutôt calculer) la vitesse initiale du projectile à sa sortie du canon. Pour cela, plusieurs formules rentrent en jeu. Il faut tout d'abord connaître l'énergie maximale que peut produire la combustion à l'intérieur de la chambre afin de pouvoir, grâce à la capacité calorifique des différents éléments, déterminer la variation de température que connaîtra le patator. Ensuite, et avec l'emploi de la loi de Gay-Lussac qui déclare qu'à volume constant, la pression est proportionnelle à la température (pV = nRT), on obtient une pression qui sera en partie appliquée sur la pomme de terre sur une certaine distance et dont on peut tirer une vitesse initiale.
Cependant, il faut tout de même considérer ce résultat avec précaution car, bien qu'il soit issu de calculs semblablement justes et précis, il a fallu, pour l'obtenir, avoir recours à plusieurs approximations et admettre plusieurs éléments qui ne peuvent être connus que par l'expérience. Par exemple, on considère que la chambre de combustion est totalement étanche, que la réaction des gaz est complète, ou encore que la totalité de l'énergie de la combustion se transforme en chaleur. Ainsi, le résultat sera forcément bien supérieur à celui que l'on obtiendrait par l'expérience.
Energie libérée par cette combustion
Afin de pouvoir calculer la trajectoire de la pomme de terre, nous avons besoin de connaître sa vitesse à la sortie du canon.
Nous avons vu précédemment que la formule d’une combustion au butane est : 2 C4H10+ 13 O2 → 8 CO2 + 10 H2O et que l’énergie de réaction de cette combustion est ER= -5 210 kJ/mol.
Ainsi, pour connaître l’énergie libérée par cette combustion, celle qui s’appliquera sur la pomme de terre, il nous faut multiplier cette énergie de réaction par le nombre de moles qui vont agir dans la combustion, donc par le cmax de la réaction, que nous pouvons calculer grâce au tableau d’avancement suivant :
 |
|---|
Calcul de cmax :
7.5 x 10-3 – 2cmax = 0 4.8 x 10-2 – 13cmax = 0
cmax =3.7x10-3 mol cmax =3.7x10-3 mol
A présent que nous connaissons la valeur de cmax, nous pouvons en tirer l'énergie libérée par le calcul suivant :
Elibérée= ER x cmax
= -5 210 x 3.7x10-3
Transformation de l'énergie en chaleur
Pour trouver la variation de température Dt, il faut d’abord passer par la capacité calorifique (Cv) de l’eau et du dioxyde de carbone, c’est-à-dire, la quantité d’énergie nécessaire pour augmenter de 1 degré (°C ou K) 1 kg de chacun de ces éléments.
En connaissant la capacité calorifique de ces deux éléments, on peut, en calculant la masse de chacun de ces produits, obtenir la variation de température qui se passera à l'intérieur de la chambre de combustion.
On a :
CV(H2O)= 1 410 J•kg-1•K-1
CV(CO2)= 650 J•kg-1•K-1
n(H2O) = 37.0x10-3mol
n(CO2) = 29.6x10-3 mol
M(H2O) = 2x1 + 16 = 18 g•mol-1
M(CO2) = 12 + 2x16 = 44 g•mol-1
Donc :
m(H2O)= 37.0x10-3 x 18 = 6.66x10-1 g
m(CO2)= 29.6x10-3 x 44 = 13.02x10-1 g
Et un capacité calorifique moyenne qui vaut :
CV(moyen) = 
= 907.2 J•kg-1•K-1
On sait que Cv = 
Donc Dt = 
soit Dt = 
= 2 260 K (ou °C, ici, cela revient au même puisque nous avons une variation de température.)
En partant d’une température initiale TI = 25 °C (ou 298K), la température finale est donc :
TF = TI + Dt = 298 + 2 260 = 2 558K
Transformation de la chaleur en pression
Grâce à cette température, il nous est maintenant possible de calculer la pression exercée sur la pomme de terre grâce à la célèbre formule PV = nRT. Puisque nous avons le volume (V=5.5x10-3 m3), les quantités de matières (n(H2O) = 37.0x10-3 mol et n(CO2) = 29.6x10-3 mol) et la température (2 558 K), on peut calculer la pression.
On a donc :
= 257.403 kPa
Pression exercée sur la pomme de terre
Sachant que la force exercée sur un corps est égale à la pression exercée dessus multipliée par sa surface, on peut estimer la force F exercée sur la pomme de terre grâce à l’aire du canon qui vaut environ 20 cm2 ou 2x10-3 m2.
On a donc :
F = 257.403x103 x 2x10–3 = 515 N
Travail des forces
On peut grâce à cette force calculer l’énergie donnée à la pomme de terre. Cette énergie, appelée travail des forces (WF), est la multiplication de la force F par la distance AB sur laquelle cette force s’exerce et par le cosinus de l’angle formé entre le vecteur F et le segment [AB] (dans notre situation, cet angle est nul car la force s'exerce le long du canon et donc dans le même sens que le segment [AB]. Le cosinus vaut donc 1).Dans notre situation, nous sommes obligés d'admettre que la force s'exerce sur une distance de 10 centimètres car, bien que le canon mesure 50 centimètres de long, cette force décroit rapidement lors de l'avancée de la pomme de terre le long du canon du fait de la diminution de pression que cela engendre dans la chambre de combustion.
On a donc :
WF = 515 x 0,10 x 1 = 51.5 J
Calcul de la vitesse initiale du projectile à sa sortie du canon
On sait que l’énergie cinétique d’un objet projeté dans les airs est égale à la moitié du produit de la masse de cet objet et du carré de sa vitesse. Or l’énergie cinétique correspond, dans notre cas au travail des forces.
Donc on a :
(Ec0=WF)
On en déduit que la vitesse initiale vaut :
Voici donc la vitesse théorique initiale du projectile à sa sortie du canon. Il faudra ensuite, par l'expérience savoir si cette vitesse est proche de la réalité ou si, à cause des approximations qui ont dues être faites lors des différents calculs, elle est trop élevée par rapport à la réalité. Le résultat que nous avons obtenu sera nécessaire pour pouvoir prédire la longueur du tir (voir ci-dessous).
Choix de l'angle du tir
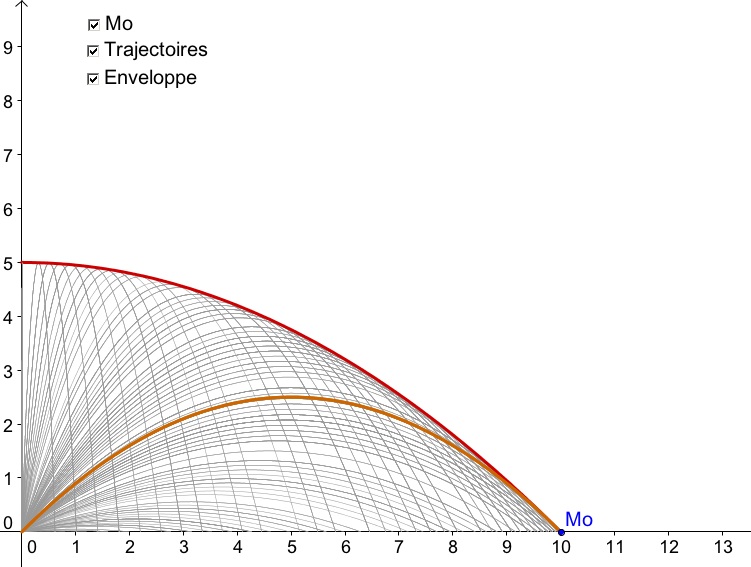
Grâce à la notion mathématique de «parabole de sécurité », il est possible de trouver la distance d’atterrissage maximale de la pomme de terre. La parabole de sécurité correspond à une enveloppe des trajectoires possibles d’un projectile. Les points « en dehors » de cette courbe ne peuvent pas être atteints. L’équation de la parabole de sécurité dépend de la hauteur initiale ainsi que de la vitesse de départ du projectile, donc fatalement, de son poids et de la gravité.
Grâce à ces quelques notions, il est possible de faire une conjecture à l’aide de Géogebra quant à l’angle de tir optimal pour obtenir une distance de tir maximale.
Vous pouvez aussi télécharger nos animations Géogébra à propos de cet angle avec un des liens ci-dessous.
Choix de l'angle (nécessite Géogébra)
On voit sur cette animation que, pour une vitesse constante de 45 m/s, l'angle de 45° semble être celui pour lequel le projectile part le plus loin.
Courbe de sécurité (nécessite Géogébra)
On a sur cette image la parabole de sécurité tracée en rouge, les différentes trajectoires d’un projectile X inconnu en gris, la trajectoire pour un angle de 45° en orange. Le point Mo appartient à la parabole de sécurité.
Il faut que Mo ait une abscisse la plus grande possible sachant que son ordonnée doit être égale à 0.
Sur cette représentation graphique, il semble que lorsque Mo a des coordonnées telles que cité précédemment, le point appartient à la parabole de sécurité ainsi qu’à la trajectoire donnée par un tir à 45°.
Il faut donc tirer avec un angle de 45° pour obtenir une longueur de tir optimale.
Equation cartésienne de la trajectoire du projectile
Pour pouvoir prévoir la portée d'un tir de patator, il faut établir l'équation de la courbe que va suivre le projectile lors de sa projection dans les airs. Trois forces rentrent alors en jeu : la gravité un vecteur vertical qui va pousser la pomme de terre vers le sol, la vecteur vitesse initiale qui est dans le sens du canon, c'est-à-dire selon un angle de 45° avec le sol, et les frottements de l'air qui vont exercer une force horizontale dans le sens inverse du vecteur vitesse mais que l'on ne va pas prendre en compte pour ne pas compliquer les calculs outre mesure.
Cette équation se définit donc avec g, la constante de gravité; v0, le vecteur vitesse au temps zéro; l’angle de tir a; et y0, la hauteur depuis laquelle le tir part.
On a l’équation cartésienne : y = 
Comment trouver cette équation?
Ce que l'on a
, le vecteur vitesse au temps t=0
, le vecteur vitesse selon le temps
M0, le point de départ du projectile
M(t), le point du projectile selon le temps
g, la norme du vecteur accélération a
, le vecteur accélération selon le temps
a, l’angle formé par v0 et i
, le vecteur position selon le temps
y0, la hauteur depuis laquelle on tire (ici, 0.35 m)
Ce que l'on en déduit
a est donc l’angle de tir (ici 45°)
v0 a pour coordonnées (v0 x cos(a) ; v0 x sin(a))
a pour coordonnées (c(t) ; y(t))
a pour coordonnées (cv(t) ; yv(t))
Dans ce problème, on ne tiendra pas compte des frottements entre la pomme de terre et l’air, car les notions que cela implique ne sont pas de notre niveau. Nous pourrons voir par l'expérience si cette omission altère de façon signifiante le résultat ou non.
Coordonnées de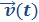 
On sait que : 
=
(par dérivation de OM(t))
Donc, 
a pour coordonnées les coordonnées dérivées de OM(t)
(c’(t) ; y’(t))
Coordonnées de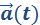 
On sait que : 
=
(par dérivation de 
)
Donc, 
a pour coordonnées les coordonnées dérivées de 
(cv’(t) ; yv’(t))
Calcul de l'équation de la courbe
Comme les frottements sont négligés, on a :
(0 ; -g)
Donc, par intégration on trouve les coordonnées du vecteur vitesse :
(k1 ; -gt+k2) (k1 et k2 étant des constantes)
Et, pour t=0 : 
=
, de coordonnées (v0 x cos(a) ; v0 x sin(a))
et 
a aussi pour coordonnées (k1; -g0+k2) (-g0 = 0)
Par conséquent k1 =v0 x cos(a) et k2 = v0 x sin(a)
et comme 
a pour coordonnées (k1 ; -gt+k2)
On a en remplaçant les constantes par leur valeur :
(v0 x cos(a) ; -gt+v0 x sin(a))
De plus, 
(c'(t) ; y'(t)) (dérivation de 
)
On a donc le système {
et, par intégration : { 
Donc, pour t=0 : { 
(
et 
étant des constantes)
or,M0(0;y0)
donc q1 = 0 et q2 = Y0
Et : 
Ce système d'équations est le système d'équations paramétriques de la trajectoire.
Conclusion
Comme : 
alors : 
et :
Donc : 
C'est l'équation Cartésienne de la trajectoire.
Grâce à cette équation, nous avons pu réaliser un petit programme géogébra que vous pouvez télécharger en cliquant sur le lien ci-dessous, et où l'on peut connaître la longueur du tir en faisant varier sa vitesse initiale.
Longueur du tir (nécessite Géogébra)
Longueur du tir
Pour connaître la longueur du tir on résout y=0, puis on fait la différence entre les deux solutions de cette équation.
y est un trinôme du degré deux de forme ac2+bc+c où a = 
, b = 
, et c = Y0 (hauteur initiale). Il va donc falloir calculer delta puis la ou les éventuelle(s) racine(s) de y=0 (si tout s'est passé comme prévu, on devrait trouver deux racines puisque nous avons un point de départ et un point d'impact de la pomme de terre).
Simplification de a,b et c
On sait que a = , que V0 = 45 m•s-1 , que a = 45°, et que Y0 = 0.35 m
Donc on a :
a = 
= 
= 
b = 
= 1
c = Y0 = 0.35
Calcul de delta
Delta est positif donc le trinôme aura deux racines (ça tombe plutôt bien!)
Calcul des racines
On sait que les deux racines de ce polynôme s'exprime par c1 = 
et c2 = 
Soit c1 =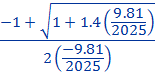 
= 
= 
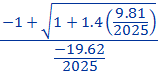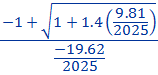
Et c2 =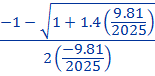 
= 
= 
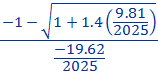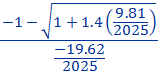
Longueur théorique du tir
Pour trouver la distance au sol parcourue par la pomme de terre lors d'un tir, il suffit maintenant de faire la différence entre les deux racines que nous venons de calculer et d'en déduire la distance qui sépare le point de départ du projectile de son point d'impact.
Donc la longueur du tir vaut : 
Soit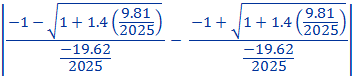 
= 
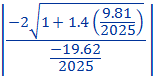
207 m
Nous avons donc réussi a déterminer par la théorie et assez précisément la longueur que devrait faire un lancer de pomme de terre avec le patator. Reste encore à vérifier par l'expérience si cette estimation est juste ou si nous avons omis trop de détails qu'il aurait fallu prendre en compte pour ne pas fausser les calculs de façon notable.